CS35 Lab3: Analysis
Run update35 to get copies of some useful files added to your cs35/labs/03 directory. You will not need to turn in any code this week. Instead you will turn in written solutions to the problems below as well as some graphs showing the results of various running time experiments.
You may work with a partner this week. However, you should work
together on each problem rather than each working on only half of the
problems. Make sure that both names are on the pages that you hand in.
- C-3.14 An array A contains n-1 unique integers in the range 0 to n-1. Thus exactly one number in this range is missing in the array. Design an O(n) time algorithm for finding this missing number. However, you are only allowed O(1) extra space. You cannot make extra arrays of size n, but you can store a constant number of extra variables.
-
Based on C-3.20 The image below shows an n by n grid that is stored in memory as a two dimensional array. The element at row i column j can be indexed in constant time using grid[i][j]. Each cell in the grid contains either a 1 or a 0 (indicated in the figure with green and white blocks). In any column, all the one's appear before any of the zeros. Given such a grid, design an O(n) algorithm for finding the column with the most ones (tallest green tower). Note there are O(n^2) cells, so you cannot check every cell in the grid.
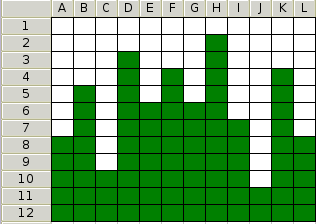
-
Consider the following algorithm that updates each element in an array of integers.
void dostuff(A, n): for i=0 to n-1: A[i] = A[i] +1I claim that the following induction proof shows that the runtime of this algorithm is O(1). Consider the base case when n=1. There is only one item to update and this can be done in constant (O(1)) time. Now assume that the algorithm runs in O(1) time for some array of size k. To show that the algorithm runs in O(1) time for arrays of size k+1, note that arrays of size k can be processed in O(1) time by our previous assumption and processing the final k+1 element can also be done in O(1) time. Since each of these two steps takes O(1) time, O(1)+O(1)=O(1) and the algorithm runs in O(1) time for all n.Something is wrong with this induction proof (Hint: consider the definition of O(g(n))). Describe the flaw and give the proper runtime.
- C-3.19 Let S be a set of n lines, such that no two are parallel and no three meet at the same point. Show by induction on the number of lines in S, that there are O(n^2) intersection points. Try sketching out the case for n=1,2,3 and 4 lines. How many new intersections does the nth line add? Finally, once you have shown this result, suppose we relax the restriction that no two lines are parallel. Draw an example where there are multiple parallel lines, but there are still O(n^2) intersections. If you live in Ohio or further West, this should be really easy.
-
Give the best big-Oh bounds on the runtime of the following functions.
Ex1(n) for(i=0; i<n; i++) a = i Ex2(n) for(i=0; i<n; i+=2) a = i Ex3(n) for(i=0; i<n*n; i++) a = i Ex4(n) for(i=0; i<n; i++) for(j=0; j<=i; j++) a = i Ex5(n) for(i=0; i<n*n; i++) for(j=0; j<=i; j++) a = i Ex6(n) k=1 for(i=0; i<n; i++) for(j=0; j<k; j++) a = j k=k*2
Perform an experimental analysis that compares the relative running times of the functions you considered in Ex1 through Ex6 above.
In running these experiments, you may need to use very different sizes of n, depending on the example being tested. Fast algorithms may not start showing any distinctions until n gets to be greater than 100,000. Slower algorithms may begin showing differences when n is nearer to 100. One really slow algorithm might not be able to process n=100 in the lifetime of the universe.
In your cs35/labs/03 directory there are some starting point files to help you with this task.
- There is a Timer class that works like a stop watch. You can start one of these objects before some code for which you want to measure the running time. Then stop it after the code you are measuring, and print the elapsed time.
- There is a test.cpp file that contains a main program that demonstrates how to use the Timer class on a particular problem.
- Note: the examples in the book use integer types for i,j, and n. For some values of n, n*n is larger than the maximum value of an integer. Instead of int n use long n for your function prototypes and local variables.
-
There is a ex4results file that shows how you can create a
text file that is readable by a script called pgraph that I made up to replace xgraph
that views your results graphically. Be sure to put your name (or names)
in the title and to label the data with an appropriate name.
To see the results do:
pgraph ex4results
- To save the graph, click the save button at the bottom, select "Postscript (*.ps)" format,
type a filename, e.g., mygraph.ps, and click save. To print this file type:
lpr mygraph.ps
on the command line