12. Dictionaries¶
All of the compound data types we have studied in detail so far — strings, lists, and tuples—are sequence types, which use integers as indices to access the values they contain within them.
Dictionaries are a different kind of compound type. They are Python’s built-in mapping type. They map keys, which can be any immutable type, to values, which can be any type, just like the values of a list or tuple.
As an example, we will create a dictionary to translate English words into Spanish. For this dictionary, the keys are strings.
One way to create a dictionary is to start with the empty dictionary and add
key-value pairs. The empty dictionary is denoted {}:
>>> eng2sp = {}
>>> eng2sp['one'] = 'uno'
>>> eng2sp['two'] = 'dos'
The first assignment creates a dictionary named eng2sp; the other
assignments add new key-value pairs to the dictionary. We can print the current
value of the dictionary in the usual way:
>>> print(eng2sp)
{'two': 'dos', 'one': 'uno'}
The key-value pairs of the dictionary are seperated by commas. Each pair contains a key and a value separated by a colon.
The order of the pairs may not be what you expected. Python uses complex algorithms to determine where the key-value pairs are stored in a dictionary. For our purposes we can think of this ordering as unpredicatable.
Another way to create a dictionary is to provide a list of key-value pairs using the same syntax as the previous output:
>>> eng2sp = {'one': 'uno', 'two': 'dos', 'three': 'tres'}
It doesn’t matter what order we write the pairs. The values in a dictionary are accessed with keys, not with indices, so there is no need to care about ordering.
Here is how we use a key to look up the corresponding value:
>>> print(eng2sp['two'])
'dos'
The key 'two' yields the value 'dos'.
12.1. Dictionary operations¶
The del statement removes a key-value pair from a dictionary. For example,
the following dictionary contains the names of various fruits and the number of
each fruit in stock:
>>> inventory = {'apples': 430, 'bananas': 312, 'oranges': 525, 'pears': 217}
>>> print(inventory)
{'oranges': 525, 'apples': 430, 'pears': 217, 'bananas': 312}
If someone buys all of the pears, we can remove the entry from the dictionary:
>>> del inventory['pears']
>>> print(inventory)
{'oranges': 525, 'apples': 430, 'bananas': 312}
Or if we’re expecting more pears soon, we might just change the value associated with pears:
>>> inventory['pears'] = 0
>>> print(inventory)
{'oranges': 525, 'apples': 430, 'pears': 0, 'bananas': 312}
The len function also works on dictionaries; it returns the number
of key-value pairs:
>>> len(inventory)
4
12.2. Dictionary methods¶
Dictionaries have a number of useful built-in methods.
The keys method takes a dictionary and returns a list of its keys.
>>> list(eng2sp.keys())
['three', 'two', 'one']
As we saw earlier with strings and lists, dictionary methods use dot notation, which specifies the name of the method to the right of the dot and the name of the object on which to apply the method immediately to the left of the dot. The parentheses indicate that this method takes no parameters.
A method call is called an invocation; in this case, we would say that we
are invoking the keys method on the object eng2sp. As we will see in a
few chapters when we talk about object oriented programming, the object on
which a method is invoked is actually the first argument to the method.
The values method is similar; it returns a list of the values in the
dictionary:
>>> list(eng2sp.values())
['tres', 'dos', 'uno']
The items method returns both, in the form of a list of tuples — one for
each key-value pair:
>>> list(eng2sp.items())
[('three', 'tres'), ('two', 'dos'), ('one', 'uno')]
The in operator checks if a key exists in the dictionary and returns True if the
key appears in the dictionary and False otherwise:
>>> 'one' in eng2sp
True
>>> 'deux' in eng2sp
False
This method can be very useful, since looking up a non-existant key in a dictionary causes a runtime error:
>>> eng2esp['dog']
Traceback (most recent call last):
File "", line 1, in
KeyError: 'dog'
>>>
12.3. Aliasing and copying¶
Because dictionaries are mutable, you need to be aware of aliasing. Whenever two variables refer to the same object, changes to one affect the other.
If you want to modify a dictionary and keep a copy of the original, use the
copy method. For example, opposites is a dictionary that contains pairs
of opposites:
>>> opposites = {'up': 'down', 'right': 'wrong', 'true': 'false'}
>>> alias = opposites
>>> copy = opposites.copy()
alias and opposites refer to the same object; copy refers to a
fresh copy of the same dictionary. If we modify alias, opposites is
also changed:
>>> alias['right'] = 'left'
>>> opposites['right']
'left'
If we modify copy, opposites is unchanged:
>>> copy['right'] = 'privilege'
>>> opposites['right']
'left'
12.4. Sparse matrices¶
We previously used a list of lists to represent a matrix. That is a good choice for a matrix with mostly nonzero values, but consider a sparse matrix like this one:

The list representation contains a lot of zeroes:
matrix = [[0, 0, 0, 1, 0],
[0, 0, 0, 0, 0],
[0, 2, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 3, 0]]
An alternative is to use a dictionary. For the keys, we can use tuples that contain the row and column numbers. Here is the dictionary representation of the same matrix:
matrix = {(0, 3): 1, (2, 1): 2, (4, 3): 3}
We only need three key-value pairs, one for each nonzero element of the matrix. Each key is a tuple, and each value is an integer.
To access an element of the matrix, we could use the [] operator:
matrix[(0, 3)]
1
Notice that the syntax for the dictionary representation is not the same as the syntax for the nested list representation. Instead of two integer indices, we use one index, which is a tuple of integers.
There is one problem. If we specify an element that is zero, we get an error, because there is no entry in the dictionary with that key:
>>> matrix[(1, 3)]
KeyError: (1, 3)
The get method solves this problem:
>>> matrix.get((0, 3), 0)
1
The first argument is the key; the second argument is the value get should
return if the key is not in the dictionary:
>>> matrix.get((1, 3), 0)
0
get definitely improves the semantics of accessing a sparse matrix. Shame
about the syntax.
12.5. Hints¶
If you played around with the fibonacci function from the Recursion and exceptions chapter, you
might have noticed that the bigger the argument you provide, the longer the
function takes to run. Furthermore, the run time increases very quickly. On one
of our machines, fibonacci(20) finishes instantly, fibonacci(30) takes
about a second, and fibonacci(40) takes roughly forever.
To understand why, consider this call graph for fibonacci with
n = 4:
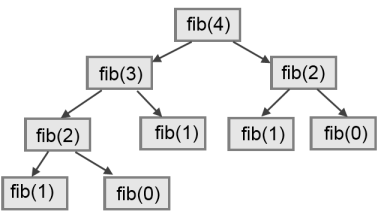
A call graph shows a set function frames, with lines connecting each frame to
the frames of the functions it calls. At the top of the graph, fibonacci
with n = 4 calls fibonacci with n = 3 and n = 2. In turn,
fibonacci with n = 3 calls fibonacci with n = 2 and n = 1.
And so on.
Count how many times fibonacci(0) and fibonacci(1) are called. This is
an inefficient solution to the problem, and it gets far worse as the argument
gets bigger.
A good solution is to keep track of values that have already been computed by
storing them in a dictionary. A previously computed value that is stored for
later use is called a hint. Here is an implementation of fibonacci
using hints:
previous = {0: 0, 1: 1}
def fibonacci(n):
if n in previous:
return previous[n]
else:
new_value = fibonacci(n-1) + fibonacci(n-2)
previous[n] = new_value
return new_value
The dictionary named previous keeps track of the Fibonacci numbers we
already know. We start with only two pairs: 0 maps to 1; and 1 maps to 1.
Whenever fibonacci is called, it checks the dictionary to determine if it
contains the result. If it’s there, the function can return immediately without
making any more recursive calls. If not, it has to compute the new value. The
new value is added to the dictionary before the function returns.
Using this version of fibonacci, our machines can compute
fibonacci(100) in an eyeblink.
>>> fibonacci(100)
354224848179261915075L
The L at the end of the number indicates that it is a long integer.
12.6. Long integers¶
Python provides a type called long that can handle any size integer
(limited only by the amount of memory you have on your computer).
There are three ways to create a long value. The first one is to compute an
arithmetic expression too large to fit inside an int. We already saw this
in the fibonacci(100) example above. Another way is to write an integer
with a capital L at the end of your number:
>>> type(1L)
The third is to call long with the value to be converted as an argument.
long, just like int and float, can convert ints, floats,
and even strings of digits to long integers:
>>> long(7)
7L
>>> long(3.9)
3L
>>> long('59')
59L
12.7. Counting letters¶
In the Strings chapter, we wrote a function that counted the number of occurrences of a letter in a string. A more general version of this problem is to form a histogram of the letters in the string, that is, how many times each letter appears.
Such a histogram might be useful for compressing a text file. Because different letters appear with different frequencies, we can compress a file by using shorter codes for common letters and longer codes for letters that appear less frequently.
Dictionaries provide an elegant way to generate a histogram:
>>> letter_counts = {}
>>> for letter in "Mississippi":
... letter_counts[letter] = letter_counts.get(letter, 0) + 1
...
>>> letter_counts
{'M': 1, 's': 4, 'p': 2, 'i': 4}
We start with an empty dictionary. For each letter in the string, we find the current count (possibly zero) and increment it. At the end, the dictionary contains pairs of letters and their frequencies.
It might be more appealing to display the histogram in alphabetical order. We
can do that with the items and sort methods:
>>> letter_items = list(letter_counts.items())
>>> letter_items.sort()
>>> print(letter_items)
[('M', 1), ('i', 4), ('p', 2), ('s', 4)]
12.8. Case Study: Robots¶
12.8.1. The game¶
In this case study we will write a version of the classic console based game, robots.
Robots is a turn-based game in which the protagonist, you, are trying to stay alive while being chased by stupid, but relentless robots. Each robot moves one square toward you each time you move. If they catch you, you are dead, but if they collide they die, leaving a pile of dead robot junk in their wake. If other robots collide with the piles of junk, they die.
The basic strategy is to position yourself so that the robots collide with each other and with piles of junk as they move toward you. To make the game playable, you also are given the ability to teleport to another location on the screen – 3 times safely and randomly thereafter, so that you don’t just get forced into a corner and loose every time.
12.8.2. Setting up the world, the player, and the main loop¶
Let’s start with a program that places the player on the screen and has a function to move her around in response to keys pressed:
#
# robots.py
#
from gasp import *
SCREEN_WIDTH = 640
SCREEN_HEIGHT = 480
GRID_WIDTH = SCREEN_WIDTH/10 - 1
GRID_HEIGHT = SCREEN_HEIGHT/10 - 1
def place_player():
x = random.randint(0, GRID_WIDTH)
y = random.randint(0, GRID_HEIGHT)
return {'shape': Circle((10*x+5, 10*y+5), 5, filled=True), 'x': x, 'y': y}
def move_player(player):
update_when('key_pressed')
if key_pressed('escape'):
return True
elif key_pressed('4'):
if player['x'] > 0: player['x'] -= 1
elif key_pressed('7'):
if player['x'] > 0: player['x'] -= 1
if player['y'] < GRID_HEIGHT: player['y'] += 1
elif key_pressed('8'):
if player['y'] < GRID_HEIGHT: player['y'] += 1
elif key_pressed('9'):
if player['x'] < GRID_WIDTH: player['x'] += 1
if player['y'] < GRID_HEIGHT: player['y'] += 1
elif key_pressed('6'):
if player['x'] < GRID_WIDTH: player['x'] += 1
elif key_pressed('3'):
if player['x'] < GRID_WIDTH: player['x'] += 1
if player['y'] > 0: player['y'] -= 1
elif key_pressed('2'):
if player['y'] > 0: player['y'] -= 1
elif key_pressed('1'):
if player['x'] > 0: player['x'] -= 1
if player['y'] > 0: player['y'] -= 1
else:
return False
move_to(player['shape'], (10*player['x']+5, 10*player['y']+5))
return False
def play_game():
begin_graphics(SCREEN_WIDTH, SCREEN_HEIGHT, title="Robots")
player = place_player()
finished = False
while not finished:
finished = move_player(player)
end_graphics()
if __name__ == '__main__':
play_game()
Programs like this one that involve interacting with the user through events such as key presses and mouse clicks are called event-driven programs.
The main event loop at this stage is simply:
while not finished:
finished = move_player(player)
The event handling is done inside the move_player function.
update_when('key_pressed') waits until a key has been pressed before moving
to the next statement. The multi-way branching statement then handles the all
keys relevent to game play.
Pressing the escape key causes move_player to return True, making
not finished false, thus exiting the main loop and ending the game. The 4,
7, 8, 9, 6, 3, 2, and 1 keys all cause the player to move in the appropriate
direction, if she isn’t blocked by the edge of a window.
12.8.3. Adding a robot¶
Now let’s add a single robot that heads toward the player each time the player moves.
Add the following place_robot function between place_player and
move_player:
def place_robot():
x = random.randint(0, GRID_WIDTH)
y = random.randint(0, GRID_HEIGHT)
return {'shape': Box((10*x, 10*y), 10, 10), 'x': x, 'y': y}
Add move_robot immediately after move_player:
def move_robot(robot, player):
if robot['x'] < player['x']: robot['x'] += 1
elif robot['x'] > player['x']: robot['x'] -= 1
if robot['y'] < player['y']: robot['y'] += 1
elif robot['y'] > player['y']: robot['y'] -= 1
move_to(robot['shape'], (10*robot['x'], 10*robot['y']))
We need to pass both the robot and the player to this function so that it can compare their locations and move the robot toward the player.
Now add the line robot = place_robot() in the main body of the program
immediately after the line player = place_player(), and add the
move_robot(robot, player) call inside the main loop immediately after
finished = move_player(player).
12.8.4. Checking for Collisions¶
We now have a robot that moves relentlessly toward our player, but once it catches her it just follows her around wherever she goes. What we want to happen is for the game to end as soon as the player is caught. The following function will determine if that has happened:
def collided(robot, player):
return player['x'] == robot['x'] and player['y'] == robot['y']
Place this new function immediately below the move_player function.
Now let’s modify play_game to check for collisions:
def play_game():
begin_graphics(SCREEN_WIDTH, SCREEN_HEIGHT)
player = place_player()
robot = place_robot()
defeated = False
while not defeated:
quit = move_player(player)
if quit:
break
move_robot(robot, player)
defeated = collided(robot, player)
if defeated:
remove_from_screen(player['shape'])
remove_from_screen(robot['shape'])
Text("They got you!", (240, 240), size=32)
sleep(3)
end_graphics()
We rename the variable finished to defeated, which is now set to the
result of collided. The main loop runs as long as defeated is false.
Pressing the key still ends the program, since we check for quit and break
out of the main loop if it is true. Finally, we check for defeated
immediately after the main loop and display an appropriate message if it is
true.
12.8.5. Adding more robots¶
There are several things we could do next:
give the player the ability to teleport to another location to escape pursuit.
provide safe placement of the player so that it never starts on top of a robot.
add more robots.
Adding the ability to teleport to a random location is the easiest task, and it has been left to you to complete as an exercise.
How we provide safe placement of the player will depend on how we represent multiple robots, so it makes sense to tackle adding more robots first.
To add a second robot, we could just create another variable named something
like robot2 with another call to place_robot. The problem with this
approach is that we will soon want lots of robots, and giving them all their
own names will be cumbersome. A more elegant solution is to place all the
robots in a list:
def place_robots(numbots):
robots = []
for i in range(numbots):
robots.append(place_robot())
return robots
Now instead of calling place_robot in play_game, call place_robots,
which returns a single list containing all the robots:
robots = place_robots(2)
With more than one robot placed, we have to handle moving each one of them. We have already solved the problem of moving a single robot, however, so traversing the list and moving each one in turn does the trick:
def move_robots(robots, player):
for robot in robots:
move_robot(robot, player)
Add move_robots immediately after move_robot, and change play_game
to call move_robots instead of move_robot.
We now need to check each robot to see if it has collided with the player:
def check_collisions(robots, player):
for robot in robots:
if collided(robot, player):
return True
return False
Add check_collisions immediately after collided and change the line in
play_game that sets defeated to call check_collisions instead of
collided.
Finally, we need to loop over robots to remove each one in turn if
defeated becomes true. Adding this has been left as an exercise.
12.8.6. Winning the game¶
The biggest problem left in our game is that there is no way to win. The robots are both relentless and indestructible. With careful maneuvering and a bit of luck teleporting, we can reach the point where it appears there is only one robot chasing the player (all the robots will actually just be on top of each other). This moving pile of robots will continue chasing our hapless player until it catches it, either by a bad move on our part or a teleport that lands the player directly on the robots.
When two robots collide they are supposed to die, leaving behind a pile of junk. A robot (or the player) is also supposed to die when it collides with a pile of junk. The logic for doing this is quite tricky. After the player and each of the robots have moved, we need to:
Check whether the player has collided with a robot or a pile of junk. If so, set
defeatedto true and break out of the game loop.Check each robot in the
robotslist to see if it has collided with a pile of junk. If it has, disgard the robot (remove it from therobotslist).Check each of the remaining robots to see if they have collided with another robot. If they have, disgard all the robots that have collided and place a pile of junk at the locations they occupied.
Check if any robots remain. If not, end the game and mark the player the winner.
Let’s take on each of these tasks in turn.
12.8.7. Adding junk¶
Most of this work will take place inside our check_collisions
function. Let’s start by modifying collided, changing the names of
the parameters to reflect its more general use:
def collided(thing1, thing2):
return thing1['x'] == thing2['x'] and thing1['y'] == thing2['y']
We now introduce a new empty list named junk immediately after the
call to place_robots:
junk = []
and modify check_collisions to incorporate the new list:
def check_collisions(robots, junk, player):
# check whether player has collided with anything
for thing in robots + junk:
if collided(thing, player):
return True
return False
Be sure to modify the call to check_collisions (currently
defeated = check_collisions(robots, player)) to include junk as a new
argument.
Again, we need to fix the logic after if defeated: to remove the new
junk from the screen before displaying the They got you! message:
for thing in robots + junk:
remove_from_screen(thing['shape'])
Since at this point junk is always an empty list, we haven’t changed the
behavior of our program. To test whether our new logic is actually working, we
could introduce a single junk pile and run our player into it, at which point
the game should remove all items from the screen and display the ending
message.
It will be helpful to modify our program temporarily to change the random
placement of robots and player to predetermined locations for testing. We plan
to use solid boxes to represent junk piles. We observe that placing a robot is
very similar to placing a junk pile, and modify place_robot to do both:
def place_robot(x, y, junk=False):
return {'shape': Box((10*x, 10*y), 10, 10, filled=junk), 'x': x, 'y': y}
Notice that x and y are now parameters, along with a new parameter that
we will use to set filled to true for piles of junk.
Our program is now broken, since the call in place_robots to
place_robot does not pass arguments for x and y. Fixing this and
setting up the program for testing is left to you as an exercise.
12.8.8. Removing robots that hit junk¶
To remove robots that collide with piles of junk, we add a nested loop to
check_collisions between each robot and each pile of junk. Our first
attempt at this does not work:
def check_collisions(robots, junk, player):
# check whether player has collided with anything
for thing in robots + junk:
if collided(thing, player):
return True
# remove robots that have collided with a pile of junk
for robot in robots:
for pile in junk:
if collided(robot, pile):
robots.remove(robot)
return False
Running this new code with the program as setup in exercise 11, we find a bug. It appears that the robots continue to pass through the pile of junk as before.
Actually, the bug is more subtle. Since we have two robots on top of each other, when the collision of the first one is detected and that robot is removed, we move the second robot into the first position in the list and it is missed by the next iteration. It is generally dangerous to modify a list while you are iterating over it. Doing so can introduce a host of difficult to find errors into your program.
The solution in this case is to loop over the robots list backwards, so
that when we remove a robot from the list all the robots whose list indeces
change as a result are robots we have already evaluated.
As usual, Python provides an elegant way to do this. The built-in function,
reversed provides for backward iteration over a sequence. Replacing:
for robot in robots:
with:
for robot in reversed(robots):
will make our program work the way we intended.
12.8.9. Turning robots into junk and enabling the player to win¶
We now want to check each robot to see if it has collided with any other robots. We will remove all robots that have collided, leaving a single pile of junk in their wake. If we reach a state where there are no more robots, the player wins.
Once again we have to be careful not to introduce bugs related to removing things from a list over which we are iterating.
Here is the plan:
Check each robot in
robots(an outer loop, traversing forward).Compare it with every robot that follows it (an inner loop, traversing backward).
If the two robots have collided, add a piece of junk at their location, mark the first robot as junk, and remove the second one.
Once all robots have been checked for collisions, traverse the robots list once again in reverse, removing all robots marked as junk.
Check to see if any robots remain. If not, declare the player the winner.
Adding the following to check_collisions will accomplish most of what we
need to do:
# remove robots that collide and leave a pile of junk
for index, robot1 in enumerate(robots):
for robot2 in reversed(robots[index+1:]):
if collided(robot1, robot2):
robot1['junk'] = True
junk.append(place_robot(robot1['x'], robot1['y'], True))
remove_from_screen(robot2['shape'])
robots.remove(robot2)
for robot in reversed(robots):
if robot['junk']:
remove_from_screen(robot['shape'])
robots.remove(robot)
We make use of the enumerate function we saw in the Lists chapter to get both the
index and value of each robot as we traverse forward. Then a reverse traversal
of the slice of the remaining robots, reversed(robots[index+1:]), sets up
the collision check.
Whenever two robots collide, our plan calls for adding a piece of junk at that
location, marking the first robot for later removal (we still need it to
compare with the other robots), and immediately removing the second one. The
body of the if collided(robot1, robot2): conditional is designed to do just
that, but if you look carefully at the line:
robot1['junk'] = True
you should notice a problem. robot1['junk'] will result in a systax error,
since our robot dictionary does not yet contain a 'junk' key. To fix this
we modify place_robot to accomodate the new key:
def place_robot(x, y, junk=False):
return {'shape': Box((10*x, 10*y), 10, 10, filled=junk),
'x': x, 'y': y, 'junk': junk}
It is not at all unusual for data structures to change as program development proceeds. Stepwise refinement of both program data and logic is a normal part of the structured programming process.
After robot1 is marked as junk, we add a pile of junk to the junk list at
the same location with
junk.append(place_robot(robot1['x'], robot1['y'], True)), and then remove
robot2 from the game by first removing its shape from the graphics window
and then removing it from the robots list.
The next loop traverses backward over the robots list removing all the robots
previously marked as junk. Since the player wins when all the robots die, and
the robot list will be empty when it no longer contains live robots, we can
simply check whether robots is empty to determine whether or not the player
has won.
This can be done in check_collisions immediately after we finish checking
robot collisions and removing dead robots by adding:
if not robots:
return ...
Hmmm… What should we return? In its current state, check_collisions is a
boolean function that returns true when the player has collided with something
and lost the game, and false when the player has not lost and the game should
continue. That is why the variable in the play_game function that catches
the return value is called defeated.
Now we have three possible states:
robotsis not empty and the player has not collided with anything – the game is still in playthe player has collided with something – the robots win
the player has not collided with anything and
robotsis empty – the player wins
In order to handle this with as few changes as possible to our present program,
we will take advantage of the way that Python permits sequence types to live
double lives as boolean values. We will return an empty string – which is
false – when game play should continue, and either "robots_win" or
"player_wins" to handle the other two cases. check_collisions should
now look like this:
def check_collisions(robots, junk, player):
# check whether player has collided with anything
for thing in robots + junk:
if collided(thing, player):
return "robots_win"
# remove robots that have collided with a pile of junk
for robot in reversed(robots):
for pile in junk:
if collided(robot, pile):
robots.remove(robot)
# remove robots that collide and leave a pile of junk
for index, robot1 in enumerate(robots):
for robot2 in reversed(robots[index+1:]):
if collided(robot1, robot2):
robot1['junk'] = True
junk.append(place_robot(robot1['x'], robot1['y'], True))
remove_from_screen(robot2['shape'])
robots.remove(robot2)
for robot in reversed(robots):
if robot['junk']:
remove_from_screen(robot['shape'])
robots.remove(robot)
if not robots:
return "player_wins"
return ""
A few corresponding changes need to be made to play_game to use the new
return values. These are left as an exercise.
12.9. Glossary¶
- dictionary
A collection of key-value pairs that maps from keys to values. The keys can be any immutable type, and the values can be any type.
- mapping type
A mapping type is a data type comprised of a collection of keys and associated values. Python’s only built-in mapping type is the dictionary. Dictionaries implement the associative array abstract data type.
- key
A data item that is mapped to a value in a dictionary. Keys are used to look up values in a dictionary.
- key-value pair
One of the pairs of items in a dictionary. Values are looked up in a dictionary by key.
- hint
Temporary storage of a precomputed value to avoid redundant computation.
- event
A signal such as a keyboard press, mouse click, or message from another program.
- event-driven program
<fill in definition here>
- event loop
A programming construct that waits for events and processes them.
- overflow
A numerical result that is too large to be represented in a numerical format.
12.10. Exercises¶
Write a program that reads in a string on the command line and returns a table of the letters of the alphabet in alphabetical order which occur in the string together with the number of times each letter occurs. Case should be ignored. A sample run of the program would look this this:
$ python letter_counts.py "ThiS is String with Upper and lower case Letters." a 2 c 1 d 1 e 5 g 1 h 2 i 4 l 2 n 2 o 1 p 2 r 4 s 5 t 5 u 1 w 2 $
Give the Python interpreter’s response to each of the following from a continuous interpreter session:
>>> d = {'apples': 15, 'bananas': 35, 'grapes': 12} >>> d['banana']
>>> d['oranges'] = 20 >>> len(d)
>>> 'grapes' in d
>>> d['pears']
>>> d.get('pears', 0)
>>> fruits = list(d.keys()) >>> fruits.sort() >>> print(fruits)
>>> del d['apples'] >>> 'apples' in d
Be sure you understand why you get each result. Then apply what you have learned to fill in the body of the function below:
def add_fruit(inventory, fruit, quantity=0): """ Adds quantity of fruit to inventory. >>> new_inventory = {} >>> add_fruit(new_inventory, 'strawberries', 10) >>> 'strawberries' in new_inventory True >>> new_inventory['strawberries'] 10 >>> add_fruit(new_inventory, 'strawberries', 25) >>> new_inventory['strawberries'] """
Your solution should pass the doctests.
Write a program called
alice_words.pythat creates a text file namedalice_words.txtcontaining an alphabetical listing of all the words found in alice_in_wonderland.txt together with the number of times each word occurs. The first 10 lines of your output file should look something like this:Word Count ======================= a 631 a-piece 1 abide 1 able 1 about 94 above 3 absence 1 absurd 2
How many times does the word,
alice, occur in the book?What is the longest word in Alice in Wonderland ? How many charactes does it have?
Copy the code from the Setting up the world, the player, and the main loop section into a file named
robots.pyand run it. You should be able to move the player around the screen using the numeric keypad and to quit the program by pressing the escape key.Laptops usually have smaller keyboards than desktop computers that do not include a seperate numeric keypad. Modify the robots program so that it uses ‘a’, ‘q’, ‘w’, ‘e’, ‘d’, ‘c’, ‘x’, and ‘z’ instead of ‘4’, ‘7’, ‘8’, ‘9’, ‘6’, ‘3’, ‘2’, and ‘1’ so that it will work on a typical laptop keyboard.
Add all the code from the Adding a robot section in the places indicated. Make sure the program works and that you now have a robot following around your player.
Add all the code from the Checking for Collisions section in the places indicated. Verify that the program ends when the robot catches the player after displaying a They got you! message for 3 seconds.
Modify the
move_playerfunction to add the ability for the player to jump to a random location whenever the0key is pressed. (hint:place_playeralready has the logic needed to place the player in a random location. Just add another conditional branch tomove_playerthat uses this logic whenkey_pressed('0')is true.) Test the program to verify that your player can now teleport to a random place on the screen to get out of trouble.Make all the changes to your program indicated in Adding more robots. Be sure to loop over the
robotslist, removing each robot in turn, afterdefeatedbecomes true. Test your program to verify that there are now two robots chasing your player. Let a robot catch you to test whether you have correctly handled removing all the robots. Change the argument from 2 to 4 inrobots = place_robots(2)and confirm that you have 4 robots.Make the changes to your program indicated in Adding ``junk``. Fix
place_robotsby moving the random generation of values forxandyto the appropriate location and passing these values as arguments in the call toplace_robot. Now we are ready to make temporary modifications to our program to remove the randomness so we can control it for testing. We can start by placing a pile of junk in the center of our game board. Change:junk = []
to:
junk = [place_robot(GRID_WIDTH/2, GRID_HEIGHT/2, junk=True)]
Run the program and confirm that there is a black box in the center of the board.Now change
place_playerso that it looks like this:def place_player(): # x = random.randint(0, GRID_WIDTH) # y = random.randint(0, GRID_HEIGHT) x, y = GRID_WIDTH/2 + 3, GRID_HEIGHT/2 return {'shape': Circle((10*x+5, 10*y+5), 5, filled=True), 'x': x, 'y': y}
Finally, temporarily comment out the random generation of
xandyvalues inplace_robotsand the creation ofnumbotsrobots. Replace this logic with code to create two robots in fixed locations:def place_robots(numbots): robots = [] # for i in range(numbots): # x = random.randint(0, GRID_WIDTH) # y = random.randint(0, GRID_HEIGHT) # robots.append(place_robot(x, y)) robots.append(place_robot(GRID_WIDTH/2 - 4, GRID_HEIGHT/2 + 2)) robots.append(place_robot(GRID_WIDTH/2 - 4, GRID_HEIGHT/2 - 2)) return robots
When you start your program now, it should look like this:
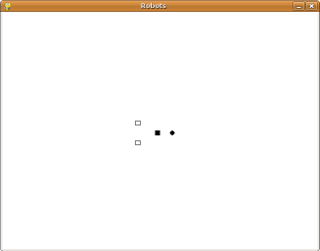
When you run this program and either stay still (by pressing the
5repeatedly) or move away from the pile of junk, you can confirm that the robots move through it unharmed. When you move into the junk pile, on the other hand, you die.Make the following modifications to
play_gameto integrate with the changes made in Turning robots into junk and enabling the player to win:Rename
defeatedtowinnerand initialize it to the empty string instead ofFalse.